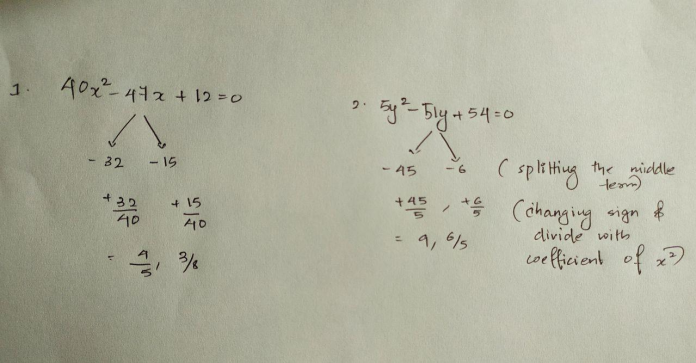Equations, a fundamental mathematical concept, play a pivotal role in banking. Their significance extends beyond theoretical mathematics to practical applications in the financial sector. Furthermore, for aspirants preparing for competitive banking exams, a thorough understanding of Quadratic Equations is crucial, as it enhances their problem-solving skills and equips them with the mathematical acumen necessary to tackle complex numerical challenges in these exams. The ability to adeptly handle Quadratic Equation can significantly boost a candidate’s performance, reflecting their competency in quantitative aptitude, a key assessment area in banking examinations.
Table of Contents
Risk Assessment and Portfolio Management
Quantifying Financial Risk
One of the primary applications of quadratic equations in banking is in risk assessment. Banking institutions are exposed to various forms of financial risk, including credit, market, and operational risks. Quadratic equations are instrumental in quantifying and modelling these risks.
For instance, using quadratic models enables banks to calculate the expected losses associated with credit defaults. By analysing the probability distribution of defaults and loss severity, banks can estimate the potential impact on their portfolios, helping them allocate adequate capital as a buffer against such losses.
Portfolio Optimisation
Quadratic optimisation models play a vital role in portfolio management. Banks often manage diverse portfolios comprising various financial assets. The objective is to optimise the allocation of assets to maximise returns while minimising risk. Quadratic equations facilitate this optimization by accounting for the covariance between asset returns, allowing banks to strike an optimal equilibrium between risk and reward.
Loan Amortisation and Mortgage Calculations
Loan Repayment Schedules
In retail banking, quadratic equations come into play when calculating loan amortisation schedules. These schedules outline the periodic repayments required to retire a loan, including principal and interest. Quadratic equations enable banks to determine the equated monthly installment (EMI) that borrowers must pay to liquidate their loans over a specified tenure.
Mortgage Pricing and Risk Assessment
For mortgage lending, quadratic equations aid in pricing and risk assessment. Banks must determine the interest rate corresponding to a borrower’s creditworthiness and the prevailing market conditions. Quadratic models can derive this rate, ensuring that it reflects the risk associated with the mortgage while remaining competitive.
Interest Rate Derivatives and Hedging
Basis Swaps and Caps
Banks use interest rate derivatives to manage their exposure to interest rate fluctuations. Quadratic equations are essential in pricing and hedging instruments such as basis swaps and interest rate caps. These instruments allow banks to mitigate the risk of adverse interest rate movements, thereby safeguarding their financial stability.
Value at Risk (VaR) Modelling
Quadratic equations are also employed in Value at Risk (VaR) modelling, a critical tool for measuring and managing market risk. VaR quantifies the potential loss in the value of a bank’s portfolio due to adverse market movements. Quadratic models, particularly GARCH (Generalized Autoregressive Conditional Heteroskedasticity) models, are instrumental in estimating the volatility of financial assets, a key parameter in VaR calculations.
Options Pricing and Trading Strategies
Black-Scholes Model
Options play a significant role in banking, both for hedging purposes and as financial instruments. The Black-Scholes, a widely used options pricing model, relies on quadratic equations. This model allows banks to determine the fair market value of options contracts and is integral to developing trading strategies involving options.
Volatility Skew and Smile
Quadratic equations also come into play when analysing the volatility skew and smile, which characterise the implied volatility of choices with different strike prices. This analysis aids in selecting appropriate options strategies and risk management techniques, allowing banks to optimise their options portfolios.
In conclusion, the significance of the Quadratic Equation in banking is undeniable. These equations are integral to a wide range of financial applications, from risk assessment and portfolio management to loan amortisation and mortgage pricing. Quadratic models and optimisation techniques enable banks to make informed decisions, manage risk, and optimise their operations in an ever-evolving financial landscape. As technology advances and data-driven decision-making becomes more prevalent, the role of quadratic equations in banking will likely grow, solidifying their status as a cornerstone of financial mathematics.